SVA : Concurrent Assertions

Concurrent Assertions

Concurrent assertions are based on clock semantics and are evaluated continuously with every clock edge. Concurrent assertions can be temporal that means usually it describes a certain behavior that spans over a time interval.

The evaluation model for concurrent assertion is based on clock and the evaluation happens only at the occurrence of a clock tick. The values of variables used in the evaluation are the sampled values. This way, a predictable result can be obtained from the evaluation, regardless of the simulator’s internal mechanism of ordering events and evaluating events. The concurrent assertions are executed in the observe region. The actions that are to be executed upon success/failure of an assertion are not executed immediately, but in the reactive region. Controlling concurrent assertion is possible from outside by using system tasks like $asserton, $assertoff, and $assertkill.

module_common_item ::= ... | assertion_item assertion_item ::= concurrent_assertion_item | deferred_immediate_assertion_item concurrent_assertion_item ::= [ block_identifier : ] concurrent_assertion_statement concurrent_assertion_statement ::= assert_property_statement | assume_property_statement | cover_property_statement | cover_sequence_statement | restrict_property_statement assert_property_statement::= assert property ( property_spec ) action_block

A concurrent assertion statement may be specified in any of the following:

• An always procedure or initial procedure as a statement
• A module,
• An interface
• A program
• A generate block
• A checker

An example of concurrent assertion is shown below.

assert property (@(posedge clk) disable iff (!reset_n) a |=> b ##1 c);

Concurrent assertions can be reset or disabled. Also it can be labelled and this label can be used in reports (”%m”) as shown above.

property prop1; @(posedge clk) disable iff (!reset_n) a |=> b ##1 c; endproperty check_1 : assert property(prop1);

Label1: assert property (prop2(rst,in1,in2)) $display("%m, passing"); else $display("%m, failed");

Concurrent assertions in sequential environment are also possible. They contain temporal behavior but embedded in a sequential environment and derive their activation from the simulation execution of the surrounding code. They contain sequential behavior and work on sampled values.

always @(posedge clk) begin case (state) mystate0: begin state <= mystate1; assert property ($past(state) == mystate4);

For concurrent assertions it is important to ensure that the defined clock behavior is glitch free. Otherwise, wrong values can be sampled. Also, if a variable that appears in the expression for clock also appears in an expression with an assertion, the values of the two usages of the variable can be different. The current value of the variable is used in the clock expression, while the sampled value of the variable is used within the assertion.

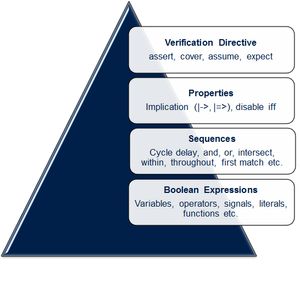
Hierarchy of concurrent assertions

Boolean expressions, sequences, properties and verification directives are the building blocks for concurrent assertions.

Boolean Layer:

The lowest level of hierarchy is the Boolean layer. In this layer, Boolean expressions are used to make basic blocks for assertion. Boolean expression does not consume time. Immediate assertions use only Boolean expressions, but concurrent use Boolean with temporal expressions. Boolean Expressions are allowed to include function calls, but certain semantic restrictions exist. That means, functions that appear in expressions which does not have output or ref arguments (const ref are allowed). Assignment operators (e.g., +=, -=) and increment/decrement operators (++/--) are not allowed inside SVA.

Supported data types in Boolean layer

• Enumerations
• time
• 4 state: integer, logic, reg
• 2-state: bit, byte, int, shortint, longint

Data types that are NOT allowed in Boolean layer:

• real, shortreal, realtime
• string
• associated arrays
• dynamic arrays
• event
• class
• chandle

Supported expressions

• boolean/logical operations
• shift/rotate operations
• arithmetic operations
• conditional expressions
• hierarchcal and selected names
• slices/indexed values
• functions

Sequence Layer

In the Sequences layer, these Boolean expressions are concatenated to each other over a period of time. This will be elaborated in the Sequence section.

Property Layer

In this layer, complex sequential expressions or Boolean expressions are used to define certain expected behaviour of the design. For more details, please refer property section.

Verification Directive layer

This layer decides on the action that the verification tool has to perform for a certain property is specified.

Different ways of writing assertions

Concurrent assertions can be written by separating out sequences, properties and call to verification directives, or can be clubbed as per the verification needs.Different ways of writing assertions are shown below

Verification directive, properties and sequences - clubbed

assert property( @(posedge clock) disable iff (!reset_n) out |=> in1 ##1 in2 );

Properties and sequences - clubbed.

property prop1 disable iff(!reset_n) out |=> in1##1 in2; endproperty: prop1 assert property (@(posedge clock) prop1);

Properties,Sequences and Verification directives - Separated.

sequence seq1 in1 ##1 in2; endsequence: seq2 property my_prop disable iff(!reset_n) out |=> my_seq; endproperty: my_prop assert property (@(posedge clk) my_prop);

Concurrent Assertions – Sampling & Clocking

Sampling mechanism in concurrent assertions eliminates possible races between RTL and assertions. It delays evaluation up to one clock cycle. The definition of a sampled value of an expression is based on the definition of a sampled value of a variable.

The variable and the corresponding sampled value can be found the below picture.

The timing model employed in a concurrent assertion specification is based on clock ticks and uses a generalized notion of clock cycles. The definition of a clock is explicitly specified by the user and can vary from one expression to another. A clock shall tick only once at any simulation time and the sampled values for that simulation time are used for evaluation of concurrent assertions.

Concurrent assertion can derive its clock from

• Default clock
• Clocking block
• Explicitly specified clock
• Clocked property/sequence
• Procedural block

The clock that is used to trigger the assertion need not be a real clock of the DUT and can also be a reference clock from TB. But it must be glitch-free. In addition, the triggering clock does not have to be a clock and an assertion can be triggered by any event. In the clocking expression of an assertion the current value of the clock is used and not the sampled one.